前言

闲来无聊，做一些简单的单链表题

题目链接如下：

206. 反转链表

题目

反转一个单链表。

示例:

输入: 1->2->3->4->5->NULL

输出: 5->4->3->2->1->NULL

进阶:

你可以迭代或递归地反转链表。你能否用两种方法解决这道题？

思路

先定义一个新链表new_list，指针cur用于遍历

反转本质就是：

将cur的下一个节点连接到new_list，即cur.next=new_list
再将new_list赋值为cur
然后将cur赋值为原本cur.next，并回到第一步继续遍历

代码

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        new_list = None
        cur = head
        while cur != None:
            tmp = cur.next
            cur.next = new_list
            new_list = cur
            cur = tmp
        return new_list

141. 环形链表

题目

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

示例 1：

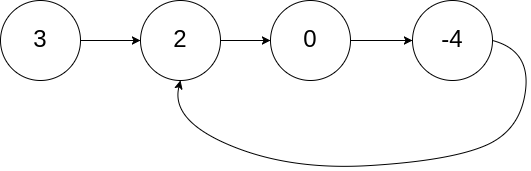
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

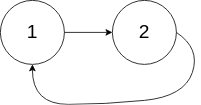
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

进阶：

你能用 O(1)（即，常量）内存解决此问题吗？

思路

检测单链表中是否有环，经典问题了，定义步长不同的两个指针，慢指针每次走一步，快指针每次走两步，如果有环，它们一定会相遇。

代码

class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        if head is None or head.next is None:
            return False
        slow = head
        fast = head.next
        while slow != fast:
            if fast.next is None or fast.next.next is None:
                return False
            else:
                fast = fast.next.next
                slow = slow.next
        return True

142. 环形链表 II

题目

给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：tail connects to node index 0
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：no cycle
解释：链表中没有环。

思路

先给结论，在上一题中，我们引入了快慢指针，在它们相遇的时候，慢指针并没有遍历完链表，所以再设置一个指针从链表头部开始遍历，这两个指针相遇的点，就是链表环的入口。

我们来证明一下：

假设进入环之前的长度为x

快慢指针相遇时，进入环之后走过的长度为a

环的长度为C

所以当它们相遇时，慢指针走了x+a步，快指针走了x+kC+a步

其中，k为正整数，表示快指针走了多少圈，但实际上走多少圈都是没关系的，相对位置没有变，所以我们为了简单，取1即可。

而又因为慢指针每次走1步，快指针每次走2步

所以快指针走过的路程是慢指针的两倍，即2(x+a)

显然x+C+a = 2(x+a)，即x = C-a

C-a又正好是慢指针还没有走完的路程

所以当快慢指针相遇时，再设置一个指针从链表头部开始遍历，每次也走1步。新指针和慢指针相遇的点，就是链表环的入口。

代码

class Solution:
    def detectCycle(self, head: ListNode) -> ListNode:
        if head is None or head.next is None:
            return None
        slow = head
        fast = head
        while fast is not None and fast.next is not None:
            fast = fast.next.next
            slow = slow.next
            if fast == slow:
                new_slow = head
                while new_slow != slow:
                    new_slow = new_slow.next
                    slow = slow.next
                return new_slow
        return None

876. 链表的中间结点

题目

给定一个带有头结点 head 的非空单链表，返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

示例 1：

输入：[1,2,3,4,5]
输出：此列表中的结点 3 (序列化形式：[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
注意，我们返回了一个 ListNode 类型的对象 ans，这样：
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.
示例 2：

输入：[1,2,3,4,5,6]
输出：此列表中的结点 4 (序列化形式：[4,5,6])
由于该列表有两个中间结点，值分别为 3 和 4，我们返回第二个结点。

提示：

给定链表的结点数介于 1 和 100 之间。

思路

很简单，略

代码

class Solution:
    def middleNode(self, head: ListNode) -> ListNode:
        if head is None or head.next is None:
            return head
        middle = head
        cur = head
        i = 1
        j = 1
        while cur is not None and cur.next is not None:
            cur = cur.next
            j += 1
            if i*2 <= j:
                i += 1
                middle = middle.next
        return middle

21. 合并两个有序链表

题目

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例：

输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

思路

很简单，略

代码

class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        cur = ListNode(0)
        if l1 is None:
            return l2
        if l2 is None:
            return l1
        l3 = cur
        while l1 is not None or l2 is not None:
            if l1 is None and l2 is not None:
                cur.next = l2
                l2 = l2.next
            elif l2 is None and l1 is not None:
                cur.next = l1
                l1 = l1.next
            elif l1.val < l2.val:
                cur.next = l1
                l1 = l1.next
            else:
                cur.next = l2
                l2 = l2.next
            cur = cur.next
        return l3.next